Científicos de Múrmansk, proponen un nuevo método semiclásico para describir sistemas moleculares complejos
Múrmansk, Múrmansk, Rusia, Europa.- La química y la física teóricas modernas se enfrentan al problema fundamental de describir la dinámica cuántica de sistemas moleculares complejos. Si bien una descripción rigurosa de la mecánica cuántica del movimiento de los núcleos moleculares es extremadamente precisa, es prácticamente inaplicable a sistemas reales debido al aumento exponencial de los costes computacionales con el aumento de los grados de libertad. Por otro lado, la mecánica clásica es relativamente económica desde el punto de vista computacional, pero no puede reproducir efectos cuánticos clave como la interferencia, la energía vibracional de punto cero y el efecto túnel. Durante varias décadas, los científicos han estado construyendo un puente de métodos semiclásicos para salvar esta brecha entre la precisión y la viabilidad computacional, buscando combinar las ventajas de ambos enfoques.
Uno de los métodos semiclásicos más utilizados es el propagador de Hermann-Kluk, propuesto por Michael Herman y Eric Kluk en 1984. Se utiliza para describir la evolución temporal de los paquetes de ondas cuánticas, en particular en dinámica molecular y espectroscopia, y permite la inclusión de importantes efectos cuánticos mediante un conjunto de trayectorias clásicas. Su idea clave es que la dinámica cuántica puede aproximarse mediante un conjunto de trayectorias clásicas, cada una equipada con un factor de fase y amplitud específico que explica los efectos cuánticos. Dentro de este enfoque, la dinámica de los paquetes de ondas se expresa como una integral sobre el espacio de fases, donde la contribución de cada trayectoria oscila con una fase determinada por la acción clásica. Esto se convierte en el principal obstáculo para los cálculos: a medida que aumenta la dimensión del sistema, la convergencia estadística del método se deteriora drásticamente y la aplicación directa del propagador de Hermann-Kluk se vuelve prácticamente imposible.
Para superar esta dificultad, se han propuesto diversas modificaciones, una de las cuales es el llamado filtrado celular o filtrado de Filinov. En la versión estándar de este enfoque, el espacio de fases se divide en celdas de tamaño finito, y la contribución de todas las trayectorias dentro de una celda se aproxima analíticamente con base en el comportamiento de la trayectoria central. Esto reduce significativamente las oscilaciones en el integrando y mejora la convergencia estadística de los cálculos. Sin embargo, el filtrado celular estándar presenta una desventaja fundamental: el tamaño de la celda se introduce como un parámetro externo, no directamente relacionado con el número de trayectorias utilizadas. Como resultado, incluso con un número infinito de trayectorias, el método no garantiza la convergencia al propagador Hermann-Kluk original, y el investigador debe analizar adicionalmente la dependencia del resultado con el ancho de la celda, lo que incrementa los costos computacionales y reduce el rigor conceptual del método.

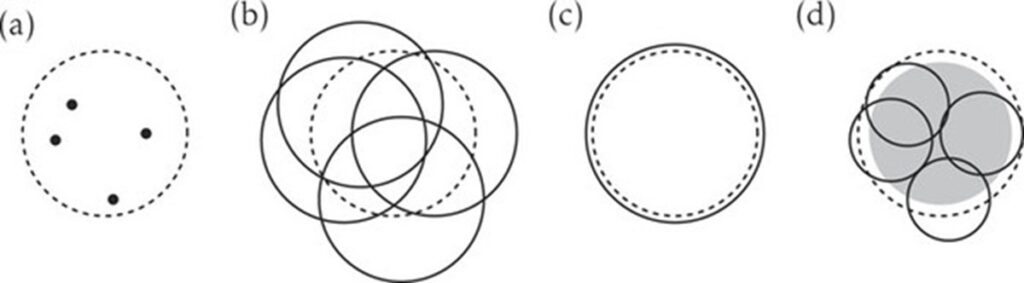
Un artículo de Fabian Kröninger, Jiri Vaníček y Sergey Antipov, investigadores del Instituto de Ciencias Químicas e Ingeniería de la Universidad Politécnica Federal de Lausana (Suiza) y del Instituto I.V. Tananaev de Química y Tecnología de Elementos Raros y Recursos Minerales del Centro Científico Kola de la Academia Rusa de Ciencias (Apatity), se ha publicado en The Journal of Chemical Physics. Los autores proponen un esquema mejorado de filtrado celular que elimina estos problemas e introduce un mecanismo internamente consistente para las transiciones entre diferentes aproximaciones semiclásicas. La idea clave del nuevo enfoque es relacionar el tamaño de las celdas del espacio de fases con el número de trayectorias utilizadas. En lugar de prefijar el ancho de la celda, los autores las escalan de tal manera que, a medida que aumenta el número de trayectorias, las celdas disminuyen automáticamente de tamaño y la densidad de muestreo de los centros de celdas se expande. Este enfoque presenta dos límites fundamentales que confieren al método una elegancia y sensibilidad físicas particulares. En el límite de un número infinito de trayectorias, el filtrado celular refinado se transforma estrictamente en el propagador Hermann-Kluck original. Esto elimina la principal desventaja conceptual del esquema estándar, que carece de esta propiedad de convergencia. En el límite opuesto, cuando se utiliza una sola trayectoria, el método degenera automáticamente en la conocida aproximación de paquetes de ondas gaussianas descongeladas, propuesta por primera vez por Edward Heller en 1975. De este modo, el nuevo esquema conecta fluidamente dos enfoques semiclásicos, previamente considerados conceptualmente distintos.
Los autores ilustran las ventajas del esquema propuesto utilizando varios problemas de modelo que abarcan regímenes dinámicos tanto integrables como caóticos. Como ejemplo de dinámica relativamente regular, consideran un modelo de una molécula de NCO colineal, en la que el paquete de ondas evoluciona sobre la superficie de un electrón excitado. Los cálculos de las funciones de autocorrelación temporal y los espectros vibracionales correspondientes muestran que el filtrado celular refinado reproduce casi a la perfección los resultados de un propagador Hermann-Kluck totalmente convergente con costos computacionales significativamente menores. Al mismo tiempo, el filtrado estándar de Filinov presenta distorsiones notables de las líneas espectrales en intervalos insuficientemente pequeños, lo que pone de relieve su sensibilidad a la elección de los parámetros.
Las ventajas del nuevo método son especialmente evidentes en el caso de la dinámica caótica, donde los métodos semiclásicos tradicionales presentan serias dificultades. Utilizando un oscilador bidimensional caracterizado por un fuerte caos, se demuestra que los cálculos directos de Hermann-Kluck producen resultados inestables y no físicos debido al crecimiento explosivo de las contribuciones de las trayectorias individuales. Por el contrario, el filtrado celular refinado suprime eficazmente estas inestabilidades mediante el filtrado adaptativo y permite una descripción razonable de la dinámica a corto plazo, lo cual es de suma importancia física, por ejemplo, al calcular espectros con ensanchamiento de línea. Además, el error estadístico del método es significativamente menor que el de los enfoques estándar, incluso para un número relativamente pequeño de trayectorias.
Un importante resultado práctico del trabajo es que el coste computacional de una sola trayectoria en el nuevo método es comparable al del propagador Hermann-Kluck tradicional y al filtrado Filinov estándar. Esto significa que la convergencia y la estabilidad mejoradas se logran no complicando la dinámica de una trayectoria individual, sino organizando de forma más inteligente el muestreo del espacio de fases y el escalado consistente de los parámetros del método.
En general, el estudio presentado demuestra cómo replantear la estructura matemática de las aproximaciones semiclásicas no solo mejora su eficiencia computacional, sino que también aclara las conexiones entre diversos métodos establecidos históricamente. El filtrado celular refinado construye eficazmente no Un puente discontinuo entre la aproximación de un solo paquete de ondas gaussianas y la descripción completa de conjuntos al estilo Hermann-Kluck, que ofrece un único parámetro de convergencia y elimina la arbitrariedad de la selección de parámetros auxiliares.
Esto hace que el método sea especialmente atractivo para su aplicación en sistemas moleculares grandes y complejos, donde el equilibrio entre precisión y viabilidad computacional es crucial: en física química fundamental (para simplificar la descripción de la evolución temporal de sistemas moleculares); en espectroscopia molecular (para modelar e interpretar espectros experimentales); en dinámica cuántica (el enfoque permite la inclusión efectiva de efectos cuánticos en métodos semiclásicos); en química computacional (para modelar sistemas moleculares complejos); y en dinámica no lineal y teoría del caos.



